Прокрастинация – это состояние, когда человек не может взяться за важные дела, например из-за отсутствия вдохновения, душевных сил или концентрации.
В данном юмористическом докладе предложены модели, которые позволяют взглянуть на механизмы этого явления.
Мы рассмотрим три модели:
Раздумья о планах привели Ахиллеса к бесконечной рекурсии, но у него лопнул стек, и он уснул. По словам Л. Питера Дойча, "итерация от человека, рекурсия от Бога". Ахиллесу нужно было выйти из рекурсии и взяться за дело (начать итерации), последовав примеру черепахи.
Вывод 1. Не надо уходить в бесконечную рекурсию планов, иначе не будет движения, как у Зенона.
где \(x(t)\) – степень готовности, \(m\) – мера инертности студента, \(F\) – усилия.
На графике показана динамика подготовки при \(F = 0\) с параметрами \(T = 10, \varepsilon = 0.02\).
За время \(T\) студент подготовится на \(\varepsilon T\). Если \(\varepsilon T \geq 1\), то дополнительные усилия не нужны.
Рассмотрим случай \(\varepsilon T < 1\). Как следует распределить усилия во времени, чтобы минимизировать суммарные усилия и достичь 1 к моменту времени \(T\)?
Обозначим \(u(t) = F(t)/m\) и сформулируем задачу оптимального управления.
\[\begin{array} {} x''(t) = u(t),\\ x(0) = 0, x'(0) = \varepsilon, \\ x(T) = 1, \\ J = \frac{1}{2}\int_0^T u^2(t)\,dt \to \min. \end{array}\]
Решение.
\[\begin{aligned}x(T) = \int_0^T x'(t)\,dt = \int_0^T\left(\varepsilon + \int_0^t u(\tau)\,d\tau\right)dt =\\ = \varepsilon T + \int_0^Td\tau \int_\tau^T u(\tau)\,dt = \varepsilon T +\int_0^T u(\tau)(T-\tau)\,d\tau.\end{aligned}\]
Задача сводится к следующей:
\[\begin{aligned}
F(u) = \varepsilon T + \int_0^T u(t)(T-t)\,dt - 1 = 0,\\
J(u) = \frac{1}{2}\int_0^T u^2(t) \to \min.
\end{aligned}
\]
Воспользуемся принципом Лагранжа [Иоффе, Тихомиров, с. 73]. Функция Лагранжа имеет вид
\[
L(u,p) = J(u) + pF(u),
\]
где \(p\) – множитель Лагранжа.
Необходимые условия экстремума:
\[
\begin{aligned}
(2)\qquad J'(u) + F'(u)p = 0,\\
F(u) = 0.
\end{aligned}
\]
Найдем производные:
\[\begin{aligned}
\langle J'(u), v\rangle = \int_0^T u(t)v(t)\,dt,\\
\langle F'(u), v\rangle = \int_0^T v(t)(T-t)\,dt.
\end{aligned}\]
Из (2) получаем
\[
u(t) + p(T - t) = 0.
\]
Подставляя \(u(t) = -p(T-t)\) в условие \(F(u) = 0\), получаем
\[
\begin{aligned}
\varepsilon T -p\int_0^T(T-t)^2\,dt - 1 = 0,\\
-p = \frac{3(1 - \varepsilon T)}{T^3},\\
u(t) = \frac{3(1 - \varepsilon T)(T-t)}{T^3}.
\end{aligned}
\]
Итак, мы нашли оптимальное управление. Соответствующая оптимальная траектория подготовки к экзамену имеет вид
\[
x(t) = \varepsilon t + \int_0^t u(s)(t - s)\,ds = \varepsilon t + \frac{(1 - \varepsilon T)}{2T^3}t^2(3T - t).
\]
На следующем графике представлено оптимальное управление.
В данном юмористическом докладе предложены модели, которые позволяют взглянуть на механизмы этого явления.
Мы рассмотрим три модели:
- Философская модель.
- Модель планирования времени.
- Модель оптимального управления.
Здесь следует оговориться, что математическая модель сама по себе точна, но тем не менее только приближённо описывает реальность. Примером может служить ньютоновская механика, имеющая известные ограничения применимости.
Философская модель
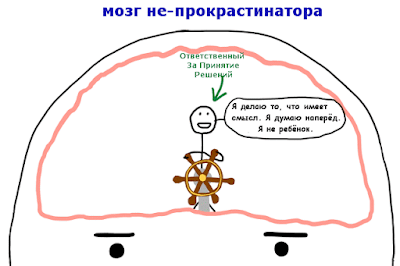
Ещё в V в. до н.э. Зенон Элейский придумал парадокс дихотомии: чтобы пройти путь, нужно пройти полпути, а для этого нужно пройти четверть пути и так до бесконечности. Другой вариант этого парадокса называется "Ахиллес и черепаха".
Представим себе, что, пока черепаха ползёт, Ахиллес размышляет: чтобы написать курсовую, нужно сначала написать введение, а для этого – сперва сделать обзор, для этого – прочитать пару статей... Хр-р-р...Раздумья о планах привели Ахиллеса к бесконечной рекурсии, но у него лопнул стек, и он уснул. По словам Л. Питера Дойча, "итерация от человека, рекурсия от Бога". Ахиллесу нужно было выйти из рекурсии и взяться за дело (начать итерации), последовав примеру черепахи.
Вывод 1. Не надо уходить в бесконечную рекурсию планов, иначе не будет движения, как у Зенона.
Модель планирования времени
Допустим, что у нас есть \(N\) задач, причём для выполнения \(i\)-й задачи требуется потратить \(l_i\) времени, и у задачи установлен срок сдачи \(t_i\). Также все задачи имеют приоритеты \(p_i\). Цель – найти оптимальный план выполнения заданий.
Составим функцию стоимости, которую мы должны минимизировать:
\[
\begin{aligned}
\qquad \int_0^T C(t)\,dt \to \min, \quad T = \sum_{i=1}^N l_i,
\\
(1)\qquad C(t) = \sum_{i=1}^N p_i \exp\left[ \underbrace{(l_i - d_i(t))}_{\text{нужно сделать}}
- \underbrace{(t_i - t)}_{\text{осталось времени}} \right].
\end{aligned}
\]
Здесь \(d_i(t)\) – время, потраченное на \(i\)-ю задачу до момента времени \(t\).
Таким образом, чем больше мы просрочиваем выполнение задания, тем больше становится функция стоимости (растёт экспоненциально). Более точно, \(i\)-е слагаемое в функции \(C(t)\) остается неизменным, когда \(i\)-е задание выполняется, и экспоненциально растёт, когда оно не выполняется.
Можно доказать [ссылка], что для достижения оптимума нужно всякий раз выполнять то задание, для которого соответствующее слагаемое в сумме (1) максимально.
Данная модель имеет одно интересное свойство. Что, если горизонт планирования \(T\) меньше суммарного времени, которое нужно потратить на выполнение всех заданий, т.е. \(T < \sum\limits_{i=1}^N l_i\)? В таком случае при построении плана на интервале длины \(T\) мы должны будем выбросить часть заданий общей длины \(\sum\limits_{i=1}^N l_i - T\). Чем больше приоритет задания, раньше срок сдачи и больше время выполнения задания, тем больше функция стоимости. Поэтому будут выброшены... наиболее важные задания! Ведь тогда функция стоимости сильнее уменьшится. Поэтому чем меньше мы будем смотреть вперёд, тем более важные задания мы будем откладывать на потом.
Вывод 2. Нужно смотреть вперёд и не забывать о наиболее приоритетных делах.
Составим функцию стоимости, которую мы должны минимизировать:
\[
\begin{aligned}
\qquad \int_0^T C(t)\,dt \to \min, \quad T = \sum_{i=1}^N l_i,
\\
(1)\qquad C(t) = \sum_{i=1}^N p_i \exp\left[ \underbrace{(l_i - d_i(t))}_{\text{нужно сделать}}
- \underbrace{(t_i - t)}_{\text{осталось времени}} \right].
\end{aligned}
\]
Здесь \(d_i(t)\) – время, потраченное на \(i\)-ю задачу до момента времени \(t\).
Таким образом, чем больше мы просрочиваем выполнение задания, тем больше становится функция стоимости (растёт экспоненциально). Более точно, \(i\)-е слагаемое в функции \(C(t)\) остается неизменным, когда \(i\)-е задание выполняется, и экспоненциально растёт, когда оно не выполняется.
Можно доказать [ссылка], что для достижения оптимума нужно всякий раз выполнять то задание, для которого соответствующее слагаемое в сумме (1) максимально.
Данная модель имеет одно интересное свойство. Что, если горизонт планирования \(T\) меньше суммарного времени, которое нужно потратить на выполнение всех заданий, т.е. \(T < \sum\limits_{i=1}^N l_i\)? В таком случае при построении плана на интервале длины \(T\) мы должны будем выбросить часть заданий общей длины \(\sum\limits_{i=1}^N l_i - T\). Чем больше приоритет задания, раньше срок сдачи и больше время выполнения задания, тем больше функция стоимости. Поэтому будут выброшены... наиболее важные задания! Ведь тогда функция стоимости сильнее уменьшится. Поэтому чем меньше мы будем смотреть вперёд, тем более важные задания мы будем откладывать на потом.
Вывод 2. Нужно смотреть вперёд и не забывать о наиболее приоритетных делах.
Модель оптимального управления
Предположим, что студент в момент времени \(t = 0\) готов к экзамену на 0%, и за время \(T\) он должен подготовиться на 100%. При этом его начальная скорость подготовки равна \(\varepsilon\).
Допустим, что динамика подготовки подчиняется 2-му закону Ньютона (силами сопротивления пренебрегаем):
\[
\begin{array}
{}mx''(t) = F(t),
\\
x(0) = 0, x'(0) = \varepsilon,
\end{array}
\]
где \(x(t)\) – степень готовности, \(m\) – мера инертности студента, \(F\) – усилия.
На графике показана динамика подготовки при \(F = 0\) с параметрами \(T = 10, \varepsilon = 0.02\).
За время \(T\) студент подготовится на \(\varepsilon T\). Если \(\varepsilon T \geq 1\), то дополнительные усилия не нужны.
Рассмотрим случай \(\varepsilon T < 1\). Как следует распределить усилия во времени, чтобы минимизировать суммарные усилия и достичь 1 к моменту времени \(T\)?
Обозначим \(u(t) = F(t)/m\) и сформулируем задачу оптимального управления.
\[\begin{array} {} x''(t) = u(t),\\ x(0) = 0, x'(0) = \varepsilon, \\ x(T) = 1, \\ J = \frac{1}{2}\int_0^T u^2(t)\,dt \to \min. \end{array}\]
Решение.
\[\begin{aligned}x(T) = \int_0^T x'(t)\,dt = \int_0^T\left(\varepsilon + \int_0^t u(\tau)\,d\tau\right)dt =\\ = \varepsilon T + \int_0^Td\tau \int_\tau^T u(\tau)\,dt = \varepsilon T +\int_0^T u(\tau)(T-\tau)\,d\tau.\end{aligned}\]
Задача сводится к следующей:
\[\begin{aligned}
F(u) = \varepsilon T + \int_0^T u(t)(T-t)\,dt - 1 = 0,\\
J(u) = \frac{1}{2}\int_0^T u^2(t) \to \min.
\end{aligned}
\]
Воспользуемся принципом Лагранжа [Иоффе, Тихомиров, с. 73]. Функция Лагранжа имеет вид
\[
L(u,p) = J(u) + pF(u),
\]
где \(p\) – множитель Лагранжа.
Необходимые условия экстремума:
\[
\begin{aligned}
(2)\qquad J'(u) + F'(u)p = 0,\\
F(u) = 0.
\end{aligned}
\]
Найдем производные:
\[\begin{aligned}
\langle J'(u), v\rangle = \int_0^T u(t)v(t)\,dt,\\
\langle F'(u), v\rangle = \int_0^T v(t)(T-t)\,dt.
\end{aligned}\]
Из (2) получаем
\[
u(t) + p(T - t) = 0.
\]
Подставляя \(u(t) = -p(T-t)\) в условие \(F(u) = 0\), получаем
\[
\begin{aligned}
\varepsilon T -p\int_0^T(T-t)^2\,dt - 1 = 0,\\
-p = \frac{3(1 - \varepsilon T)}{T^3},\\
u(t) = \frac{3(1 - \varepsilon T)(T-t)}{T^3}.
\end{aligned}
\]
Итак, мы нашли оптимальное управление. Соответствующая оптимальная траектория подготовки к экзамену имеет вид
\[
x(t) = \varepsilon t + \int_0^t u(s)(t - s)\,ds = \varepsilon t + \frac{(1 - \varepsilon T)}{2T^3}t^2(3T - t).
\]
На следующем графике представлено оптимальное управление.
На следующем графике показана оптимальная траектория.
На графике оптимального управления видно, что в момент времени \(t = 0\) нужно прикладывать максимальное усилие, которое нужно постепенно ослаблять. Чем больше усилий приложишь в начале, тем меньше будут суммарные усилия и легче будет дальше.
Вывод 3. При подготовке к экзамену нужно сразу форсировать события с максимальными усилиями, а потом можно и расслабиться.
Выводы
- Не следует заниматься излишним планированием.
- Не следует забывать о наиболее важных делах.
- Нужно прикладывать максимальные усилия в самом начале.






Комментарии
https://habr.com/ru/company/mipt/blog/446242/
Отправить комментарий